Ecología

Mediación y moderación. Dos formas distintas de interacción.

Alfonso
2018-12-05
No Comments

La mediación y la moderación son dos formas diferentes de interacción de las que no es fácil encontrar buenos ejemplos en la bibliografía. Aprovechando que el tema ha salido en clase, aprovecho para aclararlo por aquí.

Una variable mediadora intenta explicar el mecanismo por el que ocurre el efecto, mientras que una variable moderadora cambia el efecto que tiene la variable independiente sobre la dependiente. Como el post me está quedando largo, pongo un índice. Primero cuento la moderación y pongo un ejemplo con las especies de iris. Después para sólo una especie, hago un ejemplo de mediación.

Moderación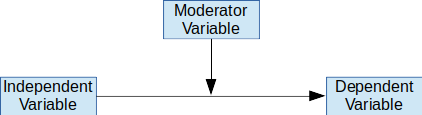
- Ejemplo de moderación con R
Mediación
- Ejemplo de mediación con R

Moderación

La moderación es lo que normalmente se entiende por «interacción» en Estadística. Es cuando una variable moderadora (Z) cambia el efecto que la variable independiente (X) tiene sobre la variable dependiente (Y).

Es decir, suponiendo que X e Y están relacionadas linearmente,

Y = a + b X

la variable moderadora puede cambiar esto ya que b depende de Z.

Y = a +b X + c Z + d XZ

Ejemplo de moderación con R e iris

Lo primero es comprobar el efecto directo de la variable independiente (Sepal.Length) sobre la variable dependiente (Petal.Length).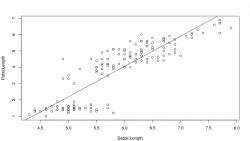

### direct relationship lmC <- lm(Petal.Length ~ Sepal.Length, data = iris) summary(lmC)
### Plot plot(Petal.Length ~ Sepal.Length, data = iris) abline(lmC)

Coefficients:
             Estimate Std. Error t value Pr(>|t|) 
(Intercept) -7.10144 0.50666 -14.02 <2e-16 ***
Sepal.Length 1.85843 0.08586  21.65 <2e-16 ***

Residual standard error: 0.8678 on 148 degrees of freedom
Multiple R-squared: 0.76, Adjusted R-squared: 0.7583 
F-statistic: 468.6 on 1 and 148 DF, p-value: < 2.2e-16

Se observa una fuerte relación (luego veremos que mal entendida) entre la longitud de los sépalos y de los pétalos. Lo siguiente es comprobar el efecto moderador de la variable Species.

### Moderation effect lmZ <- lm(Petal.Length ~ Sepal.Length + as.numeric(Species) + I(Sepal.Length * as.numeric(Species)), data = iris) summary(lmZ)

Coefficients:
                                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)                           -6.91282    0.76764  -9.005 1.08e-15 ***
Sepal.Length                           1.36959    0.14659   9.343  < 2e-16 ***
as.numeric(Species)                    3.12118    0.33548   9.304  < 2e-16 ***
I(Sepal.Length * as.numeric(Species)) -0.29266    0.05889  -4.970 1.85e-06 ***

Residual standard error: 0.3915 on 146 degrees of freedom
Multiple R-squared:  0.9518,	Adjusted R-squared:  0.9508 
F-statistic: 961.1 on 3 and 146 DF,  p-value: < 2.2e-16

Se observa que hay interacción y que todas las variables analizadas tienen un efecto significativo por separado y por su interacción. También se puede ver que el modelo es mejor que el anterior, ya que R² ha aumentado bastante.

Los resultados se pueden representar utilizando base R o con ggplot.

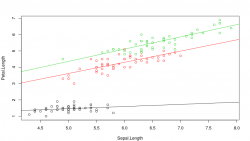Base R plot

### Partial linear models set <- subset(iris, Species == "setosa") ver <- subset(iris, Species == "versicolor") vir <- subset(iris, Species == "virginica")

lmset <- lm(Petal.Length ~ Sepal.Length, data = set) lmver <- lm(Petal.Length ~ Sepal.Length, data = ver) lmvir <- lm(Petal.Length ~ Sepal.Length, data = vir)

summary(lmset) summary(lmver) summary(lmvir)

### Plot plot(Petal.Length ~ Sepal.Length, col = as.numeric(Species), data = iris) abline(lmset, col = 1) abline(lmver, col = 2) abline(lmvir, col = 3)

ggplot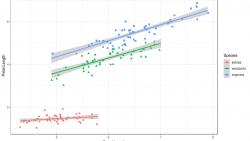

library(ggplot2) ggplot(data = iris, aes(x = Sepal.Length, y = Petal.Length, col = Species, shape = Species)) + # geom_point(size = 3) + geom_jitter(size = 2) + geom_smooth(method = 'lm',formula = y ~ x) + theme_bw()

Mediación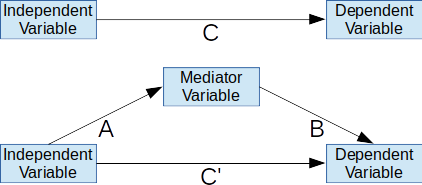

Para que exista mediación es necesario que:

Haya un efecto C, efecto directo entre la variable independiente (X) y la dependiente (Y).
Haya un efecto A entre la variable independiente y la variable mediadora (M).
Haya un efecto B entre la variable mediadora y la variable dependiente.

En ese caso la duda es cuanto efecto C queda como C’ (efecto residual) si tenemos en cuenta el efecto que pasa a través de la variable mediadora.

El efecto C lo podemos estimar en un modelo lineal a partir de la pendiente y la probabilidad (p) de que sea al azar. Para decir que hay un efecto p tiene que ser menor de 0.05, que va a ser nuestro nivel de significación.

Modelo 1: Y = a₁ + C X , p₁ < 0.05

Modelo 2: M = a₂ + A X, p₂ < 0.05

Modelo 3: Y = a₃ + B M, p₃ < 0.05

Donde C, A y B representan las pendientes de la recta, cuanto mayor sea, mayor es el efecto de X en Y, de X en M o de M en Y respectivamente.

Una vez que los tres modelos anteriores son significativos (p < 0.05), lo que nos queda por saber es cuando del efecto inicial de X en Y se mantiene al tener en cuente el efecto de M en Y.

Modelo 4: Y = a₄ + C’ X + B M, p_c’ = ??

donde se pueden dar dos opciones:

que p_c’ < 0.05, moderación parcial.
que p_c’ ≥ 0.05, moderación total.

En ambos casos la pendiente C’ debería ser menor que la pendiente C. En el primer caso, la moderación parcial significa que parte del efecto de X sobre Y, pasa a través de M, pero no todo. En el segundo caso, la moderación total, es que todo el efecto pasa a través de la variable moderadora.

Ejemplo de moderación con R e iris.

Para el ejemplo voy a utilizar los datos «iris» de longitud y anchura de pétalos y sépalos en Iris versicolor. Ya hemos visto en el ejemplo de mediación, que no tendría sentido hacerlo para las tres especies juntas.

Voy a explorar la posibilidad de mediación de la longitud de los pétalos entre la longitud de los sépalos y la anchura de los pétalos. Es decir, viendo si el efecto que tiene la longitud de los sépalos en la anchura de los pétalos es directo o si pasa por la longitud de los pétalos.

Una cosa importante es no confundir la moderación estadística con la moderación causal. El que algo sea significativo estadísticamente no es suficiente para considerar que hay una relación causa – efecto (también pasa con la mediación, la correlación y cualquier otro test estadístico).

Modelo 1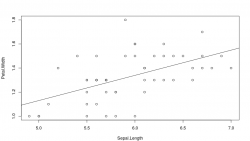

### Iris versicolor ver <- subset(iris, Species == "versicolor")

### Plot plot(Petal.Width ~ Sepal.Length, data = ver) abline(lmC)

### direct relationship lmC <- lm(Petal.Width ~ Sepal.Length, data = ver) summary(lmC)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.08326    0.27592   0.302    0.764    
Sepal.Length  0.20936    0.04631   4.521 4.04e-05 ***

Residual standard error: 0.1673 on 48 degrees of freedom
Multiple R-squared:  0.2986,	Adjusted R-squared:  0.284 
F-statistic: 20.44 on 1 and 48 DF,  p-value: 4.035e-05

Se puede ver que existe un efecto de la longitud de los sépalos sobre la anchura de los pétalos. El modelo es regularcillo, ya que sólo explica el 28 % de la varianza (R²), aunque es claramente significativo (p = 0,000004).

Modelo 1: Y = 0.083 + 0.209 X

Modelo 2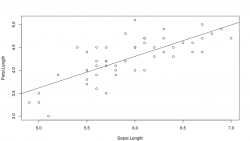

Para comprobar que hay mediación necesitamos que los otros dos modelos también sean significativos.

### Mediator Petal.Width (A) lmA <- lm(Petal.Length ~ Sepal.Length, data = ver) summary(lmA)

### Plot plot(Petal.Length ~ Sepal.Length, data = ver) abline(lmA)

Coefficients:
             Estimate Std. Error t value Pr(>|t|) 
(Intercept)  0.18512 0.51421 0.360 0.72 
Sepal.Length 0.68647 0.08631 7.954 2.59e-10 ***

Residual standard error: 0.3118 on 48 degrees of freedom
Multiple R-squared: 0.5686, Adjusted R-squared: 0.5596 
F-statistic: 63.26 on 1 and 48 DF, p-value: 2.586e-10

Modelo 2: M = 0.185 + 0.686 X

El modelo 2 es también muy claro (R² = 0.5596 y p << 0.05).

Modelo 3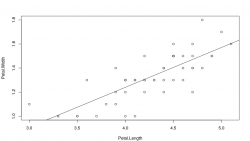

lmB <- lm(Petal.Width ~ Petal.Length, data = ver) summary(lmB)

### Plot plot(Petal.Width ~ Petal.Length, data = ver) abline(lmB)

Coefficients:
              Estimate Std. Error t value Pr(>|t|) 
(Intercept)   -0.08429 0.16070 -0.525 0.602 
Petal.Length   0.33105 0.03750  8.828 1.27e-11 ***

Residual standard error: 0.1234 on 48 degrees of freedom
Multiple R-squared: 0.6188, Adjusted R-squared: 0.6109 
F-statistic: 77.93 on 1 and 48 DF, p-value: 1.272e-11

Modelo 3: Y = -0.084 + 0.331 M

El modelo 3 es todavía mejor, explicando el 61 % de la varianza.

¿hay mediación o no?

Con los tres modelos anteriores ya sabemos que hay mediación ya que los tres modelos son significativos.

Lo que vamos a ver ahora es hasta donde llega esta mediación o el valor de C’ o el efecto de X sobre Y teniendo en cuenta que parte de dicho efecto pasa a través de M.

### Mediator Petal.Width (C2) lmC2 <- lm(Petal.Width ~ Sepal.Length + Petal.Length, data = ver) summary(lmC2)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.01561    0.20446   0.076    0.939    
Sepal.Length -0.04149    0.05218  -0.795    0.430    
Petal.Length  0.36542    0.05731   6.376 7.25e-08 ***

Residual standard error: 0.1238 on 47 degrees of freedom
Multiple R-squared:  0.6239,	Adjusted R-squared:  0.6079 
F-statistic: 38.98 on 2 and 47 DF,  p-value: 1.046e-10

Se puede observar que:

La pendiente del efecto de la longitud de los sépalos sobre la anchura de los pétalos ha cambiado de
- de C = 0.209 , claramente significativa (p = 0,000004), en el modelo 1.
- a C’ = -0.041, no significativa (p = 0.43) en este modelo.

Es decir se ha perdido el efecto de la longitud de los sépalos y se puede decir que existe una mediación total por parte de la longitud de los pétalos. Todo el efecto de X sobre Y pasa a través de M.

O dicho de otra manera, el efecto de la longitud de los sépalos sobre la anchura de los pétalos se pierde al tener en cuenta el efecto de la longitud de los pétalos, lo que supone que la longitud de los pétalos afecta a la longitud de los pétalos y es la longitud de los pétalos la que afecta a la anchura de los mismos.

Sólo recuerda que aunque haya mediación estadística, eso no significa que haya mediación causal o que la causa real sea esa.